Detailed Balance Learning

なぜContrastive Divergence Learningだとうまくいく ?

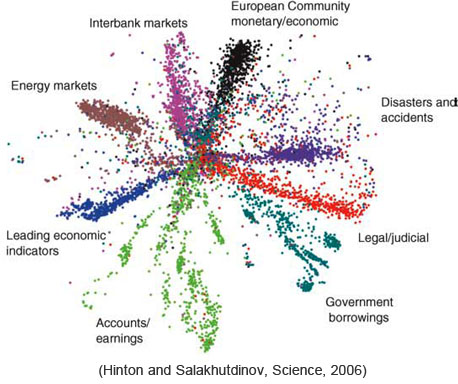
image

Hintonら(2006)は高次元パラメータをもつ階層ボルツマンマシンを大規模データを用いて学習させることに成功した。 この学習アルゴリズムにContrastive Divergence Learningが用いられており、Hintonらは これが重要なファクターであることを示唆したが、このContrastive Divergence Learningの理論背景 は明確ではなかった。

Detailed Balance Learning(DBL)

既約なマルコフ連鎖は，唯一の定常分布をもつ。 しかし、マルコフ連鎖の訪れる状態数が大きいとき、その定常分布を陽に求めることは困難であり、定常分布がサンプルを生成する真の分布に近づくようにマルコフ連鎖のパラメータを学習させることは難しい。

本研究では、このようなマルコフ連鎖の定常分布を真の分布に近づけるための新しい学習法としてDetailed Balance Learning (DBL) を提案する。

ボルツマンマシンなどの離散分布においては、しばしば、同時分布を定義した時の正規化定数をパラメータの関数として陽に表現することが困難になる。 このようなモデルにおいて条件付き分布は、例えば、各離散変数が二値であれば二項分布であるように容易に求めることができる。 ここで提案するDBLは、このような条件付き分布を用いたギプスサンプリングによるマルコフ連鎖にも適用できるため、ボルツマンマシンなどの正規化定数の計算が困難な離散変数の分布の学習に適用できる。

また、この学習法はContrastive Divergence Learning (CDL)と密接な関係をもつ。

計算機実験

モデル分布が真の分布を表現可能な場合

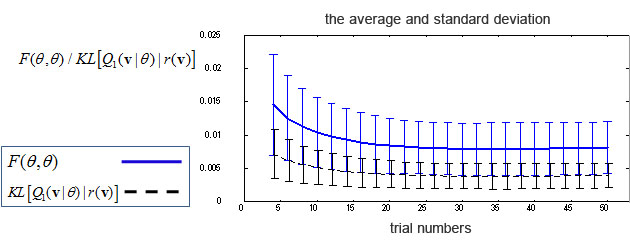
image
  • 真の分布：RBM (観測変数4次元, 隠れ変数3次元) (パラメータは乱数で決定)
  • モデル分布：RBM (観測変数4次元, 隠れ変数3次元) (初期パラメータは乱数で決定)
  • サンプル数：1000点
  • 学習則：DBL (ステップ2の実行には準ニュートン法を用いた)

モデル分布が真の分布を表現不可能な場合

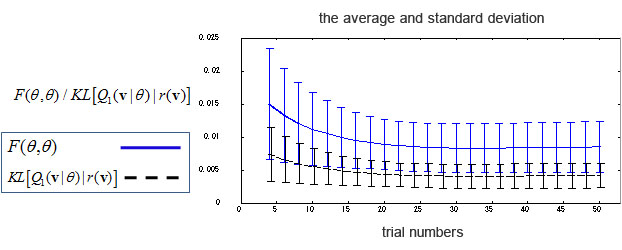
image
  • 真の分布：RBM (観測変数4次元, 隠れ変数5次元) (パラメータは乱数で決定)
  • モデル分布：RBM (観測変数4次元, 隠れ変数3次元) (初期パラメータは乱数で決定)
  • サンプル数：1000点
  • 学習則：DBL (ステップ2の実行には準ニュートン法を用いた)

今後の目標

本研究では，マルコフ連鎖の定常分布を学習する方法としてDBLを提案し、DBLがCDLと密接な関係をもつことを示した。 今後、DBLの学習速度、収束性の改善を検討する予定である。